算法设计与实现 王晓东
题目描述:
用多边形顶点的逆时针序列表示凸多边形,即P={v0,v1,…,vn-1}表示具有n条边的凸多边形。
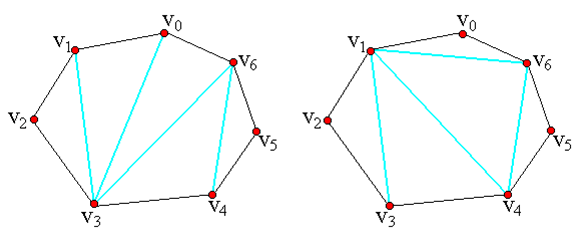
给定凸多边形P,以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分,使得即该三角剖分中诸三角形上权之和为最小。
解题思路:
若凸(n+1)边形P={v0,v1,…,vn-1}的最优三角剖分T包含三角形v0vkvn,1≤k≤n-1,则T的权为3个部分权的和:三角形v0vkvn的权,子多边形{v0,v1,…,vk}和{vk,vk+1,…,vn}的权之和。可以断言,由T所确定的这2个子多边形的三角剖分也是最优的。因为若有{v0,v1,…,vk}或{vk,vk+1,…,vn}的更小权的三角剖分将导致T不是最优三角剖分的矛盾。
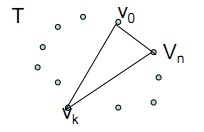
那么我们定义一个t[i][j],1<=i<=j<=N,为凸子多边形{ vi-1,vi,…,vj}的最优三角剖分所对应的权函数值,即其最优值。据此定义,要计算的凸(n+1)边形P的最优权值为t[1][n]。
t[i][j]的值可以利用最优子结构性质递归地计算。当j-i≥1时,凸子多边形至少有3个顶点。由最优子结构性质,t[i][j]的值应为t[i][k]的值加上t[k+1][j]的值,再加上三角形vi-1vkvj的权值,其中i≤k≤j-1。由于在计算时还不知道k的确切位置,而k的所有可能位置只有j-i个,因此可以在这j-i个位置中选出使t[i][j]值达到最小的位置。由此,t[i][j]可递归地定义为:
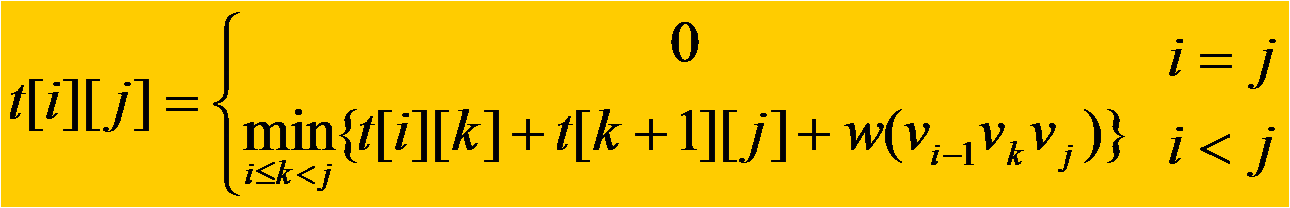
对于要求的t[1][n],可以用通过由下至上的,从链长(多边形的边)为2开始计算,每次求t[i][j]的最小值,并且记录最小值所对应的K值,根据最优子结构的性质,逐步向上就可以求出t[1][n]的最小值。
类似的,求三角划分顶点的乘积的最小值问题,也是一样的。
代码实现:
#include#define N 6 //顶点数/边数int weight[][N] = { { 0,2,2,3,1,4},{ 2,0,1,5,2,3},{ 2,1,0,2,1,4},{ 3,5,2,0,6,2},{ 1,2,1,6,0,1},{ 4,3,4,2,1,0}};int t[N][N]; //t[i][j]表示多边形{Vi-1VkVj}的最优权值int s[N][N]; //s[i][j]记录Vi-1到Vj最优三角剖分的中间点Kint get_weight(const int a, const int b, const int c){ return weight[a][b] + weight[b][c] + weight[c][a];}void minest_weight_val(){ int i,r,k,j; int min; for (i = 1; i < N; i++) { t[i][i] = 0; } for (r = 2; r < N; r++) { for (i = 1; i < N-r+1; i++) { j = i + r -1; min = 9999; //假设最小值 for (k = i; k < j; k++) { t[i][j] = t[i][k] + t[k+1][j] + get_weight(i-1,k,j); if (t[i][j] < min) //判断是否是最小值 { min = t[i][j]; s[i][j] = k; } } t[i][j] = min; //取得多边形{Vi-1,Vj}的划分三角最小权值 } }}void back_track(int a, int b){ if (a == b) return; back_track(a,s[a][b]); back_track(s[a][b]+1,b); //记得这是要加一 printf("最优三角: V%d V%d V%d.\n",a-1,s[a][b],b);}int main(){ minest_weight_val(); printf("result:%d\n",t[1][N-1]); back_track(1,5); return 0;} 2013/9/3 10:06